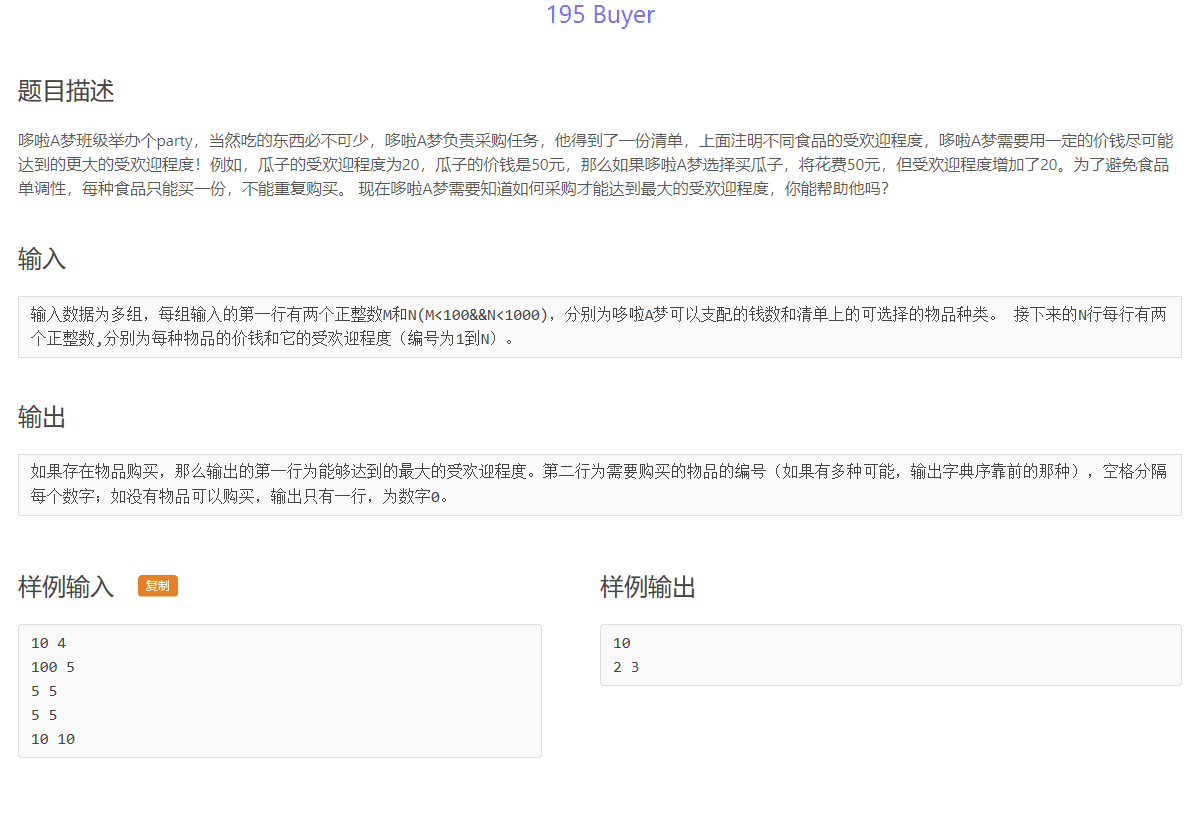
解题思路

当j-w[i]>=0时 f[i][j]=max(f[i-1][j] , v[i]+f[i-1][j-w[i])

当j-w[i]<0时 f[i][j]=f[i-1][j]

通过公式建立动态规划表

用回溯法求最优解

思路

0—1背包类问题：有N件物品和一个容量为V的背包。第i件物品的价格（即体积，下同）是w[i]，价值是c[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

相当于用f[i][j]表示前i个背包装入容量为v的背包中所可以获得的最大价值。

对于一个物品，只有两种情况

　　一: 第i件不放进去，这时所得价值为:f[i-1][v]

　　二: 第i件放进去，这时所得价值为：f[i-1][v-c[i]]+w[i]

状态转移方程为：f[i][v] = max(f[i-1][v], f[i-1][v-w[i]]+c[i])

#include<iostream>
using namespace std;
int main()
{
    int s,n;
    while(cin>>s>>n)
    {
        int w[1000]={0},v[1000]={0},a[100][100]={0},i,j,c[101]={0},k;
        k=1;
        for(i=1;i<=n;i++)
        {
            cin>>w[i]>>v[i];
        }
        for(i=1;i<=n;i++)
        {
            for(j=1;j<=s;j++)
            {

                if(j-w[i]>=0)
                {
                    if(a[i-1][j]>=(a[i-1][j-w[i]]+v[i]))
                    {
                        a[i][j]=a[i-1][j];

                    }
                    else
                        a[i][j]=a[i-1][j-w[i]]+v[i];

                }
                else
                    a[i][j]=a[i-1][j];
            }  
        }

        if(a[n][s]!=0)
        {
        cout<<a[n][s]<<endl;
        for(i=n,j=s;i>=1&&j>=1;)
        {
            if(a[i][j]>a[i-1][j])
            {
            c[k]=i;
            k++;

                j=j-w[i];
                i=i-1;

            }
            else
            {
                i=i-1;
            }


        }

    for(i=100;i>=0;i--)
    {
        if(c[i]>0)
        {
        cout<<c[i];
        if(i!=1)
            cout<<" ";
        }

    }
        }
        else
            cout<<"0";
        cout<<endl;

    }
    return 0;
}