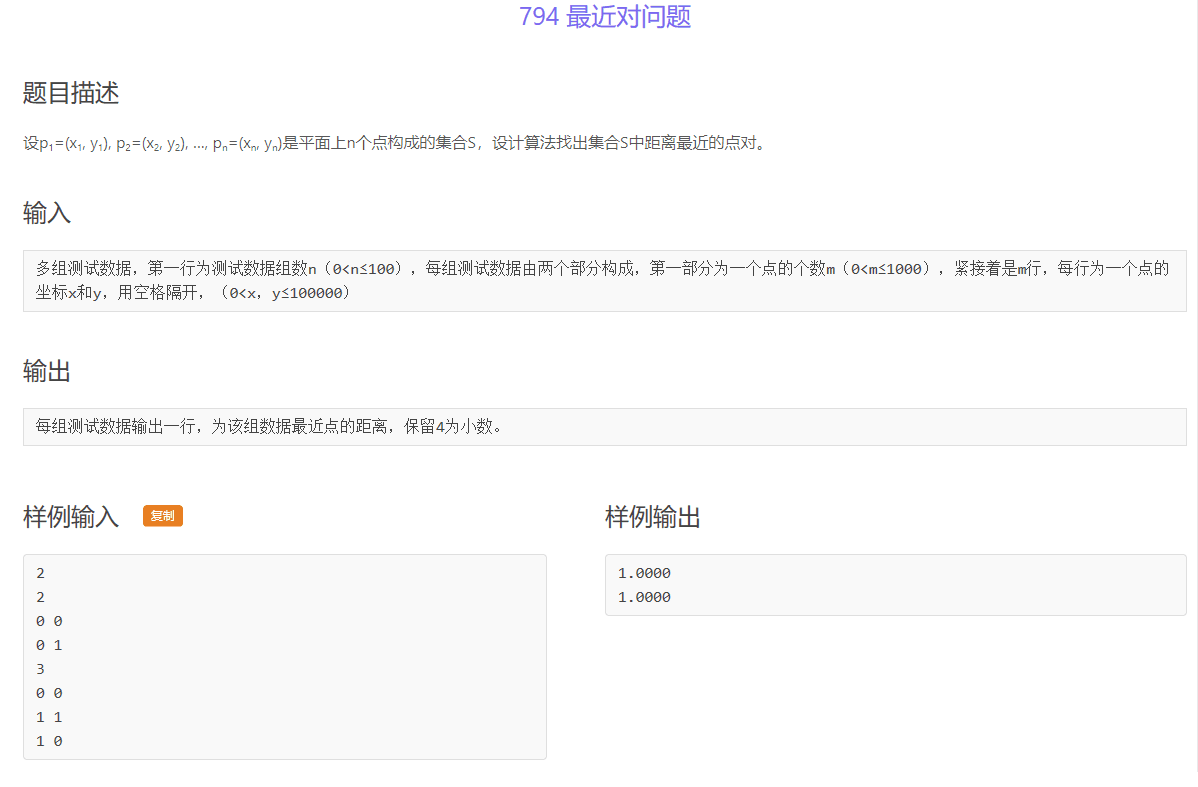
思路

蛮力法
#include<iostream>
#include<stdio.h>
#include<math.h>
using namespace std;
double Distance(double x1,double y1,double x2,double y2)
{
double dis=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));//两点之间的距离公式
return dis;
}
int main()
{
int n,i,j,m;
double x1[1001],y1[1001];
cin>>n;
while(n--)
{
cin>>m;
for(i=0;i<m;i++)
{
cin>>x1[i]>>y1[i];
}
double min=99999999;
double t;
for(i=0;i<m;i++)
{
for(j=i+1;j<m;j++)
{
t=Distance(x1[i],y1[i],x1[j],y1[j]);
if(t<min)
{
min=t;
}
}
}
printf("%.4lf\n",min);
}
return 0;
}
分治思想
#include <iostream>
#include<stdio.h>
#include <math.h>
using namespace std;
//定义结构体表示集合S中的 点的坐标
struct point{
int x, y;
};
double Closest(point S[], int low, int high); //实现求最近对距离
double Distance(point a, point b); //求两点之间距离
int Partition(point r[], int first, int end); //划分【课本P62】
void QuickSort(point r[], int first, int end); //快速排序【课本P63】
//实现求最近对距离
double Closest(point S[], int low, int high){
double d1, d2, d3, d;
int mid, i, j, index;
point P[1005]; //存放点集合 P1和P2
//如果只有两个点,返回这两个点间的距离
if (high - low == 1) {
return Distance(S[low], S[high]);
}
//如果有三个点,求最近点对距离
if (high - low == 2) {
d1 = Distance(S[low], S[low + 1]);
d2 = Distance(S[low + 1], S[high]);
d3 = Distance(S[low], S[high]);
if ((d1 < d2) && (d1 < d3)) return d1;
else if (d2 < d3) return d2;
else return d3;
}
mid = (low + high) / 2; //计算中间点
d1 = Closest(S, low, mid); //递归求解子问题①
d2 = Closest(S, mid + 1, high); //递归求解子问题②
if (d1 <= d2) d = d1; //已下为求解子问题③
else d = d2;
index = 0;
for (i = mid; (i >= low) && (S[mid].x - S[i].x < d); i--) //建立点集合P1
P[index++] = S[i];
for (i = mid + 1; (i <= high) && (S[i].x - S[mid].x < d); i++) //建立点集合P2
P[index++] = S[i];
//对集合P1、P2按y坐标升序排列
QuickSort(P, 0, index - 1);
//依次处理集合P1和P2中的点
for (i = 0; i < index; i++){
for (j = i + 1; j < index; j++){
if (P[j].y - P[i].y >= d) //超出y坐标的范围,点P[i]处理完毕
break;
else {
d3 = Distance(P[i], P[j]);
if (d3 < d)
d = d3;
}
}
}
return d;
}
//求两点之间距离
double Distance(point a, point b){
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
int Partition(point r[], int first, int end){ //划分
int i = first, j = end; //初始化待划分区间
while (i < j) {
while (i < j && r[i].y <= r[j].y) j--; //右侧扫描
if (i < j) {
point temp = r[i]; r[i] = r[j]; r[j] = temp; //将较小记录交换到前面
i++;
}
while (i < j && r[i].y <= r[j].y) i++; //左侧扫描
if (i < j) {
point temp = r[i]; r[i] = r[j]; r[j] = temp; //将较大记录交换到后面
j--;
}
}
return i; // 返回轴值记录的位置
}
void QuickSort(point r[], int first, int end){ //快速排序
int pivot;
if (first < end) {
pivot = Partition(r, first, end); //划分,pivot是轴值在序列中的位置
QuickSort(r, first, pivot - 1); //求解子问题1,对左侧子序列进行快速排序
QuickSort(r, pivot + 1, end); //求解子问题2,对右侧子序列进行快速排序
}
}
int main()
{
//输入按x坐标升序排列的n个点的集合
int N;
cin>>N;
for(int j=0;j<N;j++)
{
point S[1005];
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>S[i].x>>S[i].y;
}
double minDist = Closest(S, 0, n - 1);
printf("%.4lf\n",minDist);
}
return 0;
}

