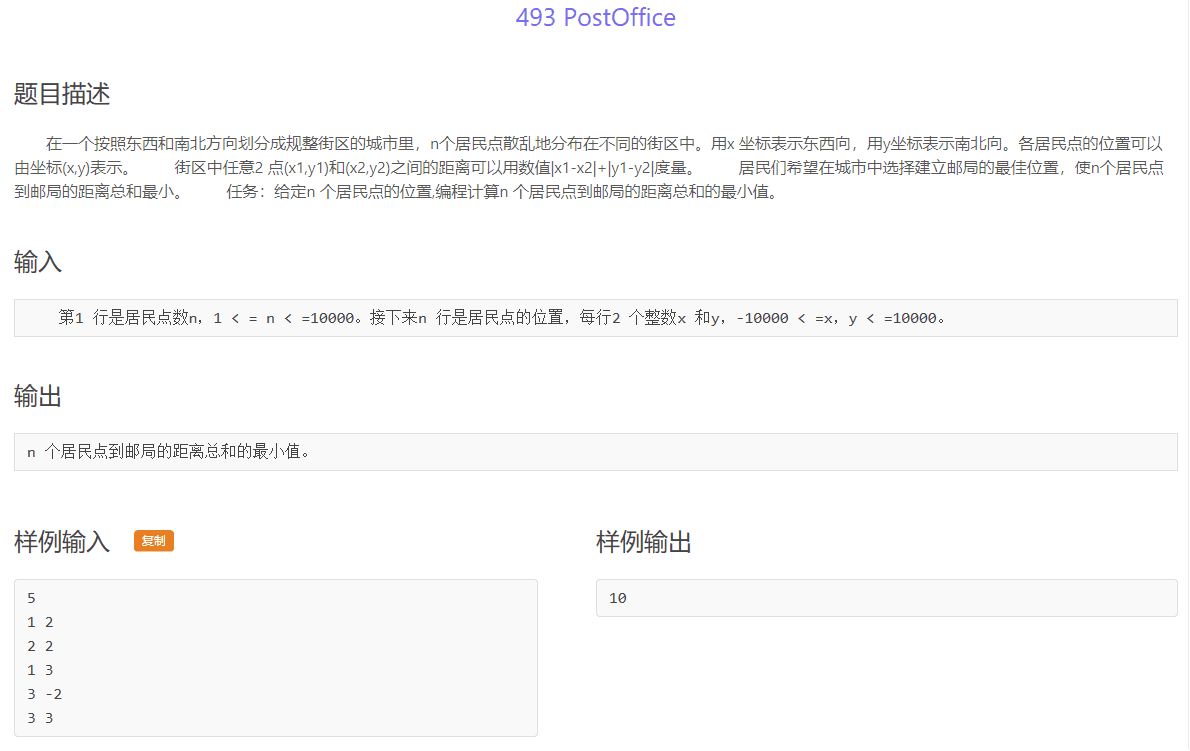
思路：

与两点一线找最短距离的思路相似，我们可以类比此题。 我们先这样思考，在一维坐标上有一系列的点，找一个点让这些点到它的距离最短，从两个点开始分析，只要点在两点之间距离都最小；若三个点，则最短距离就是相距最远距离的两点的差值，此时这个点就应该选中间那个点；同理若有多个点，毫无疑问最短距离就是各点对中值点的差值之和。 所以，对于此题我们将其先按X轴升序排列找到X轴方向的最短距离，然后在以Y轴升序找Y轴方向的最短距离，它们之和就是最终的最短距离。

#include<iostream>
#include<algorithm>
#include<math.h>

using namespace std;


int main()
{
    int x[10000], y[10000];
    int n, i, sum = 0;
    cin >> n;
    for (i = 0; i < n; i++)
    {
        cin >> x[i] >> y[i];
    }
    sort(x, x + n);
    sort(y, y + n);
    int X = x[n / 2], Y = y[n / 2];
    for (i = 0; i < n; i++)
    {
        sum += abs(x[i] - X) + abs(y[i] - Y);
    }
    cout << sum << endl;
    return 0;
}